This post discusses my project about a C++ compile-time math library.

Chapter 0

Introduction

Programming a calculator

When you think about it, programming a calculator while learning a programming language is something so classic.
Such a thing was one of my exercises back in my days at school.

By default, we use dedicated math libraries provided for the programming language and this works really fine most of the time because those libraries were heavily tested for correctness and against error-proneness. You can rely on those implementations to a certain degree.

After a while, you probably reach a higher level of knowledge in algorithms and data structures and you think about implementing a special math function like the logarithm function, for example, all by yourself.

There are valid arguments for implementing the core algorithm of a math function.
Let’s take for instance the following standard Mercator projection

When implementing this algorithm in a single function to use it in a heavy computational load, it would be bad to implement it exactly like this by using the existing math library. The proper way would be to optimize and derive a more efficient series expansion out of this and then implement it afterward.

At this point, you can either search for existing implementation examples. But if it is a very specialized formula then you have to deal with the mathematical models.

The calcupiler project will go for the last mentioned and this is one example where the project turned out to be super challenging over time.

Because … surprise surprise… there is a ton of mathematical analysis involved. It is not the implementation of equations itself but the evaluation of those, the proof of concept that gives me a headache.

Don’t get me wrong, I love challenges, and the more difficult it becomes the more excited I get.

calcupiler is a project which will evolve probably over a long period of time.
Not only because of its difficulty but because of my limited free time I can sacrifice for this project as well.

It will start with basic compile time functions like ln(x), factorial(n), … and go later for very special formulas.

The name calcupiler

As you probably correctly guessed the name is a combination of two words named calculator and compiler.

Sourcecode on GitHub

https://github.com/IboschTonosch/calcupiler

There is not much code yet and I am still building up the basics

Most important notes to run the code:

• The minimum required is C++ 20
• Tested on GCC releases:
  • 11.3 (x64)
  • 8.1 (ARM64)

Chapter 1

Definizione del problema

The word ‘problem’

If you get confused with the word ‘problem’. Any project is a problem at the beginning that wants to be solved.
That means a problem in such a case is not bad it is good. Keep that in mind 😉

Purpose of the calcupiler

calcupiler is going to be a C++ template library that will precalculate math functions during compile time and provide static numerical data for the run time.

This will increase computation performance by using the precalculated values. The compile time calculation however only works if the provided function arguments are constant as well. Any data that is not known yet cannot be calculated at compile time.

Here is an example:

// Inside a template class named Math<T>
...
// calculates the factorial of a given integral number at compile time
static constexpr T factorial_of_integral(const T& n)
{
    return k < 2 ? 1 : n * factorial_of_integral(n - 1)
}
...

// Inside any source file
...
void fun()
{
    // calculate the factorial of 5 -> evaluation is at compile time -> GOOD!
    constexpr auto result = Math<long>::factorial_of_integral(5)

    // calculate the factorial of 5 -> the given argument is not a constant -> evaluation at run-time!
    auto value = 5; // this value is not constant
    constexpr auto const& result = Math<long>::factorial_of_integral(n)
}

The constexpr specifier enables function evaluation at compile time. If n is however not const then the evaluation is done at run-time

If you want the user to be forced to evaluate these functions only at compile time then use the consteval specifier.

When you use Visual Studio, you can hover over the result variable and intellisence will show you the calculated result. This means partial compilation is even done at design time depending on what development environment you use. This also means you can check the results while implementing the logic and do corrections if the result is not as expected. Or you use the API as a calculator without running it. Pretty neat when you ask me.

Requirements for a custom math function

When implementing a series expansion for instance which is used to approximate a mathematical equation you don’t only have to validate the mathematical side but the computational side as well. The reason is that the mathematical equation represents a world in a perfect condition, however, the reality consists of errors which can be classified into the following types

• Systematic errors
  These types of errors occur systematically, which means they always occur under certain conditions and can always be predicted. The prediction is only possible if the error parameters and the conditions in which they occur are known. Systematic errors are most welcome when compensating for errors.
  –
• Random errors
  No one wants these types of errors. They occur randomly and can not be accurately predicted. To compensate for such errors you have to include probability in the calculation and balance the severity of the error considering the best-case and worst-case scenarios.
  –
• Human errors
  In the coding world, bugs are human errors. They are systematic errors when known and random errors when obviously unknown. If fixing the bug is uneconomic, the standard way would be to implement compensation. If the bug can be fixed easily then the error will be excluded from any calculation afterward.
  

Unit Testing

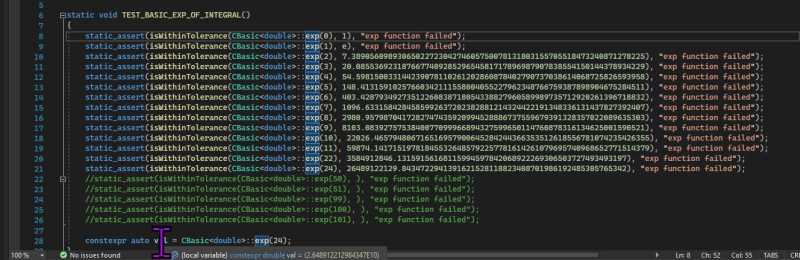
A way to validate an implementation is to create unit tests.
Creating test cases is very time-consuming. Testing and validating usually take more time than the math implementation itself.

The test cases must include error calculation for the errors mentioned before. The simplest way is to put a bias by defining a minimum and a maximum value,

For example the function

will have the following bias

where x’ is x without errors and ε is the error

we then define a bias of let’s say 0.000001 and we get

Precision

It is important to define the precision of the calculation. What precision can you guarantee with the math library?

Is it only integral or can you guarantee a floating point precision of 10E^-6 for example?

The global definition of precision is strongly related to the handling of error bias as mentioned before.

This can become an issue when an iterative calculation is done. A very small error can sum up and the final floating point accuracy suffers in such cases.

A good example is the calculation of large-scale nonlinear systems. Numerical errors add up successively which can end up with a wrong result.

So giving a defined precision for one function doesn’t guarantee the same precision in the end result when using this function on large-scale computation.

Here is an example of a small 2 x 2 matrix whose each element is a series expansion

and calculating the determinant of A would look like this

both sides of the subtraction should cancel each other out which results in 0.

Large-scale matrices however can have sizes larger than 1000 x 1000

Specialization

Once the basic functions like ln(x), sin(x), exp(x) … etc. are implemented and tested, I am going to include more specialized functions for specific applications and I am curious how far I can go without ever using run-time evaluation.

Chapter X

… coming soon …