Save intervals inside a binary tree and use it later for overlapping checks.
This data structure is kept to a minimum. Because once the concept is understood, any further extensions will be quite easy.
Provided functions will be: Adding an interval and checking for overlaps.
To have a better understanding let’s create a case example.
Say we have six different intervals
| Interval | from – to |
| X1 | 2.2 – 5.3 |
| X2 | 4.1 – 8.2 |
| X3 | 9.0 – 9.2 |
| X4 | 10.9 – 15.0 |
| X5 | 0.1 – 2.1 |
| X6 | 9.1 – 10.3 |
Visually it would look like this with the interval X6 not added yet
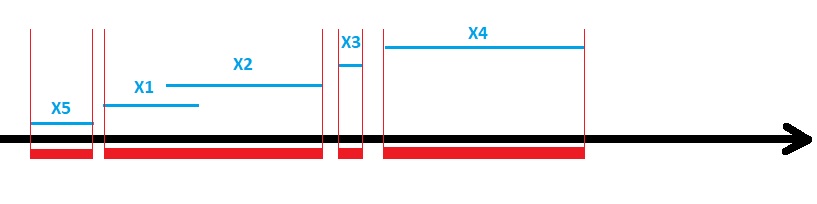
The blue lines are the individual intervals listed in the table before. The red lines show the overall coverage by unifying all intervals together.
To map this programmatically we will use a binary tree as a data structure. The tree will have leaves and each leaf will be treated as a single object which contains the following properties.
| : Property : | : Description : |
| Parent Leaf | Contains the reference to its parent leaf |
| Left Child | Contains the reference to its left child leaf |
| Right Child | Contains the reference to its right child leaf |
| Low Value | Contains the start value of the interval |
| High Value | Contains the end value of the interval |
This can be used to implement a leaf class later with the listed properties. We also need a tree class that handles all leaves.
Add a Leaf
Now, this is how the algorithm works.
- Add a new leaf to the tree
- Beginning from the root leaf …
- If leaf does not exist
- Create a new leaf
- Assign the properties
- Finish
- If newLeaf.lowValue < currentLeaf->highValue
- If left child exists
- Move to left child leaf
- Reapeat from step 4
- Else repeat from step 3
- If left child exists
- Else
- If right child exists
- Move to right child leaf
- Repeat from step 4
- Else repeat from step 3
- If right child exists
- Finish
Keep in mind that this algorithm ensures that all interval objects will still exist. It doesn’t unify all intervals to one or remove redundant intervals.
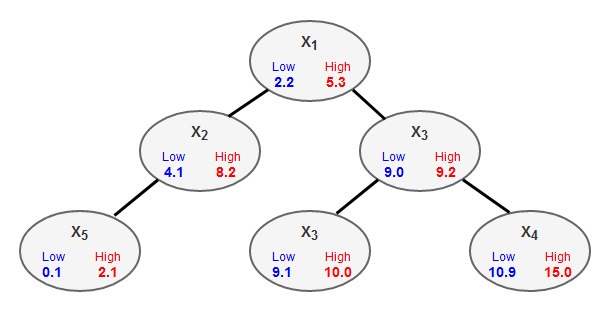
A close depiction of what we want to accomplish shows the following image where the intervals X1 to X5 have been added to the binary tree in ordered sequence {X1, … ,Xn}
Check for overlap
When checking an overlap you have to provide an interval to search for. So lets define a new interval
| Interval | from – to |
| Xsearch | 9.8 – 10.4 |
When traversing through the binary tree you have to check an interval comparison logic on each interval leaf
We give the variables the following letters
Xsearch(lowValue) = low value of the search interval = Ls
Xsearch(highValue) = high value of the search interval = Hs
Xi(lowValue) = low value of the interval within the tree = Li
Xi(highValue) = low value of the interval within the tree = Hi
The following conditions will be programmatically applied
Equality: bool anyEqual = l == L || l == H || h == L || h == H
Low value is insidebool lowInside = l > L && l < H
High value is insidebool highInside = h > L && h < H
Full overlap checkbool fullOverlap = l < L && h > H
That’s it. If any of those conditions are true then there is an overlap otherwise the traversing will continue until the last leaf has been hit.
The traversing works the same way as adding a new leaf except you don’t add the leaf but apply the conditions.
Code
here is the full code example I wrote in c++.
There are 5 code blocks intended for five different files
IntervalLeaf.h
IntervalLeaf.cpp
IntervalTree.h
IntervalTree.cpp
main.cpp
I didn’t provide any of those files to download but solely as code blocks in this post.
Just copy the following codes and put them into the appropriate files named in the code block title
IntervalLeaf.h
This header file contains the class definition for the leaf object.
#pragma once
#include <memory>
class IntervalLeaf
{
private:
IntervalLeaf* parent = nullptr;
IntervalLeaf* leftChild = nullptr;
IntervalLeaf* rightChild = nullptr;
private:
double lowValue = 0.0;
double highValue = 0.0;
double maxValue = 0.0;
public:
/// <summary>
/// Constructs a new leaf with the given intervall boundaries
/// </summary>
/// <param name="parent">The parent leaf</param>
/// <param name="lowValue">The low value of the interval</param>
/// <param name="highValue">The high value of the interval</param>
IntervalLeaf(IntervalLeaf* parent, const double lowValue, const double highValue)
: parent(parent), lowValue(lowValue), highValue(highValue)
{}
IntervalLeaf(IntervalLeaf* leaf) {};
~IntervalLeaf()
{
if (parent != nullptr)
{
delete(parent = nullptr);
}
if (leftChild != nullptr)
{
delete(leftChild = nullptr);
}
if (rightChild != nullptr)
{
delete(rightChild = nullptr);
}
}
IntervalLeaf(const IntervalLeaf& rhs)
: parent(rhs.parent)
, leftChild(rhs.leftChild)
, rightChild(rhs.rightChild)
, lowValue(rhs.lowValue)
, highValue(rhs.highValue)
{}
IntervalLeaf(IntervalLeaf&& rhs) noexcept
: parent(std::exchange(rhs.parent, nullptr))
, leftChild(std::exchange(rhs.leftChild, nullptr))
, rightChild(std::exchange(rhs.rightChild, nullptr))
, lowValue(rhs.lowValue)
, highValue(rhs.highValue)
{}
IntervalLeaf& operator=(const IntervalLeaf& rhs)
{
parent = rhs.parent == nullptr ? nullptr : rhs.parent;
leftChild = rhs.leftChild;
rightChild = rhs.rightChild;
lowValue = rhs.lowValue;
highValue = rhs.highValue;
return *this;
}
IntervalLeaf& operator=(IntervalLeaf&& rhs) noexcept
{
std::swap(parent, rhs.parent);
std::swap(leftChild, rhs.leftChild);
std::swap(rightChild, rhs.rightChild);
lowValue = rhs.lowValue;
highValue = rhs.highValue;
return *this;
}
IntervalLeaf* add(const double lowValue, const double highValue);
IntervalLeaf* overlapsWith(const double lowValue, const double highValue);
};I tried to apply some c++ guidelines for example with the rule of 5 by overriding constructors and operators. You don’t necessarily need these extensions to run this application but it is strongly recommended to hold to these guidelines.
IntervalLeaf.cpp
Contains the implementation and source code of the leaf class
#include "IntervalLeaf.h"
IntervalLeaf* IntervalLeaf::add(const double lowValue, const double highValue)
{
auto leaf = new IntervalLeaf(this, lowValue, highValue);
if (lowValue < this->highValue)
{
if (this->leftChild == nullptr)
{
this->leftChild = leaf;
}
else
{
this->leftChild->add(lowValue, highValue);
}
}
else
{
if (this->rightChild == nullptr)
{
this->rightChild = leaf;
}
else
{
this->rightChild->add(lowValue, highValue);
}
}
return leaf;
}
IntervalLeaf* IntervalLeaf::overlapsWith(const double lowValue, const double highValue)
{
const double L = this->lowValue;
const double H = this->highValue;
const double l = lowValue;
const double h = highValue;
const bool anyEqual = (l == L || l == H || h == L || h == H);
const bool lowInside = (l > L && l < H);
const bool highInside = (h > L && h < H);
const bool fullOverlap = (l < L&& h > H);
if (anyEqual || lowInside || highInside || fullOverlap)
{
return this;
}
else
{
if (this->leftChild != nullptr && lowValue < this->leftChild->highValue)
{
return this->leftChild->overlapsWith(lowValue, highValue);
}
else if (this->rightChild != nullptr)
{
return this->rightChild->overlapsWith(lowValue, highValue);
}
else
{
return nullptr;
}
}
}IntervalTree.h
Contains the class definition for the tree object. The tree object manages all leaves.
#pragma once
#include "IntervalLeaf.h"
#include <memory>
class IntervalTree
{
private:
IntervalLeaf* rootLeaf;
public:
IntervalTree() = default;
IntervalTree(const double lowValue, const double highValue)
{
*rootLeaf = IntervalLeaf(nullptr, lowValue, highValue);
}
~IntervalTree()
{
delete(rootLeaf);
rootLeaf = nullptr;
}
IntervalTree(const IntervalTree& rhs)
: rootLeaf(rhs.rootLeaf)
{}
IntervalTree(IntervalTree&& rhs) noexcept
: rootLeaf(std::exchange(rhs.rootLeaf, nullptr))
{}
IntervalTree operator=(const IntervalTree& rhs)
{
return * this = rhs;
}
IntervalTree operator=(IntervalTree&& rhs) noexcept
{
std::swap(rootLeaf, rhs.rootLeaf);
return *this;
}
void addIntervall(const double lowValue, const double highValue);
bool isOverlap(const double lowValue, const double highValue);
};IntervalTree.cpp
Contains the implementations of the tree class
#include "IntervalTree.h"
void IntervalTree::addIntervall(const double lowValue, const double highValue)
{
if (rootLeaf == nullptr)
{
auto&& leaf = new IntervalLeaf(nullptr, lowValue, highValue);
rootLeaf = leaf;
}
else
{
rootLeaf->add(lowValue, highValue);
}
}
bool IntervalTree::isOverlap(const double lowValue, const double highValue)
{
return rootLeaf != nullptr && rootLeaf->overlapsWith(lowValue, highValue) != nullptr;
}main.cpp
I put the test logic samples directly into the main.cpp for demonstration purposes. The test does instantiate the tree class adds five intervals to the tree and does four overlap checks. The comments tell you whether the overlap check result should be true or false and you can compare this with the result value.
#include "IntervalLeaf.h"
#include "IntervalTree.h"
#include <iostream>
int main()
{
// Example
// #########################################################
// Initialize tree
auto p_tree = new IntervalTree();
// Add new interval
auto lowValue = 12.3;
auto highValue = 17.42;
p_tree->addIntervall(lowValue, highValue);
// Add new interval
lowValue = 1.0;
highValue = 5.34;
p_tree->addIntervall(lowValue, highValue);
// Add new interval
lowValue = 10.03;
highValue = 11.11;
p_tree->addIntervall(lowValue, highValue);
// Add new interval
lowValue = 0.2;
highValue = 26.00;
p_tree->addIntervall(lowValue, highValue);
// Add new interval
lowValue = 200.12;
highValue = 501.63;
p_tree->addIntervall(lowValue, highValue);
// Here you can add further intervals into the tree
// lowValue = {start value of your interval}
// highValue = {end value of your interval}
// p_tree->addIntervall(lowValue, highValue);
// ---------------------------------------
// Search interval overlap
lowValue = 30;
highValue = 33;
bool isOverlap = p_tree->isOverlap(lowValue, highValue); // false expected
// Search interval overlap
lowValue = 1;
highValue = 3;
isOverlap = p_tree->isOverlap(lowValue, highValue); // true expected
// Search interval overlap
lowValue = 80;
highValue = 200.119;
isOverlap = p_tree->isOverlap(lowValue, highValue); // false expected
// Search interval overlap
lowValue = -30;
highValue = 33;
isOverlap = p_tree->isOverlap(lowValue, highValue); // true expected
// You can add further overlap checks here like following....
// lowValue = {start value of your interval}
// highValue = {end value of your interval}
// isOverlap = p_tree->isOverlap(lowValue, highValue);
// Very important. Always ensure to free any reserved heap memory
delete(p_tree = nullptr);
}