The matrix spiral – IboshTonosh

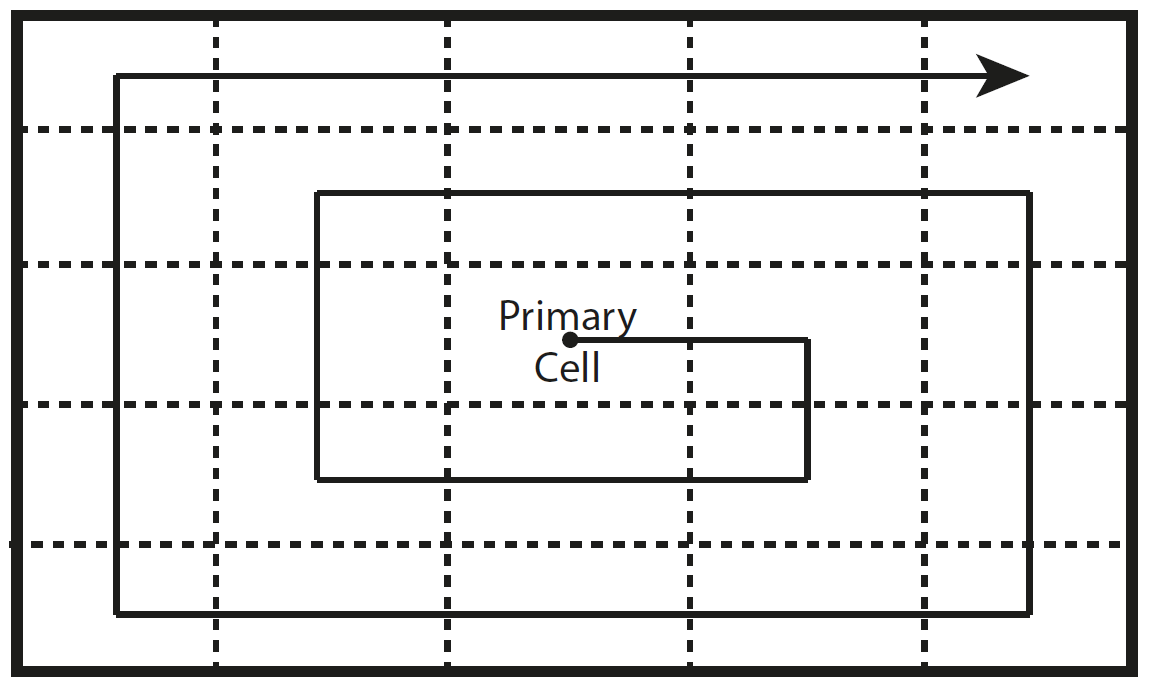
An algorithm that follows a spiral pattern to pass through each cell object in a two-dimensional matrix starting from the center cell.

Imagine the following problem. You programmed a two-dimensional field that will be divided into sectors or cells. Now you want a pointer that starts from the center cell and walks through each cell in a spiral shape like this

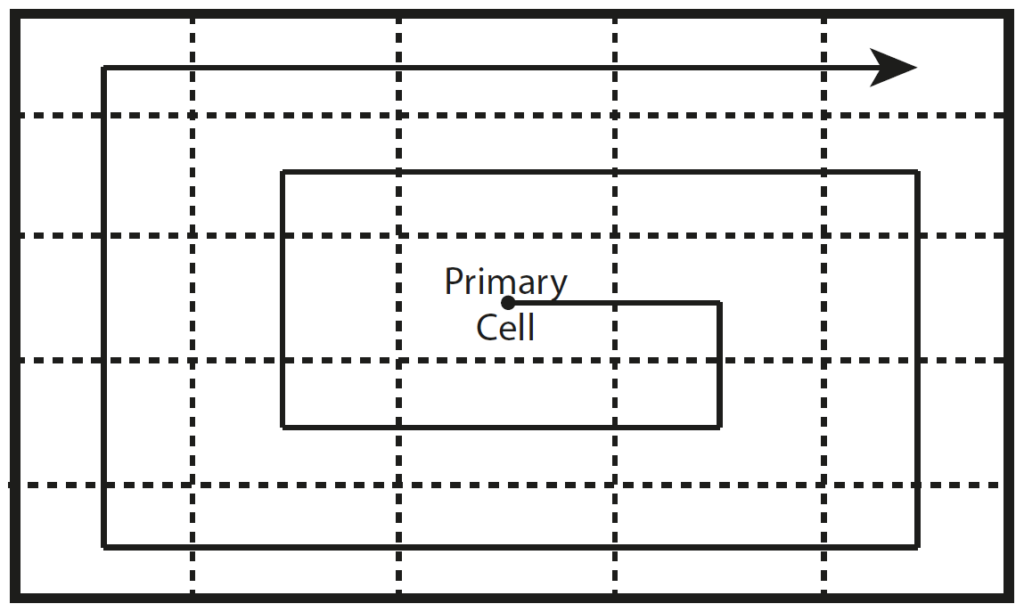
As you probably recognized, this algorithm works only on uneven numbers of rows and columns and the number of rows and columns must be equal.

So for example the following matrices will work
M_3,3, M_5,5, M_7,7, M_9,9

These ones will not work
M_2,2, M_5,7, M_6,6, M_4,2

Mathematical Model

To create a reliable algorithm for this issue, we have to define a mathematical model.
So we begin with the mathematical description of the matrix first.

The number of cells in the matrix in this use case can be described by the following sequence

$c_n = 1, 9, 25, 49, 81, ... \quad \forall n \in \mathbb{N}$

As we already know, the number of rows and columns is equal. With that, we can now create the sequence identity, which is

$c_n = (2n-1)^2$

When starting from the center cell as seen in the picture before, then the sequence of cell steps looks like this

$c_n = 1, 1, 2, 2, 3, 3, 4, 4, ... \quad \forall n \in \mathbb{N}$

It looks very similar to a super simple sum, except that every second increment must be canceled out.

So the +1 must be canceled out whenever n reaches an uneven number beginning with n = 0

$S_n = \displaystyle\frac{1}{2}\sum_{i=0}^{n} \left((-1)^i+1\right) \quad \forall i \in \mathbb{N}$

Now we also include the positive and negative steps into the sequence. X-Y direction is not considered yet.

What we want is…

$S_n = 1, 1, -2, -2, 3, 3, -4, -4, ... \quad \forall n \in \mathbb{N}$

Here is a depiction of the sequence to have a better idea of how it works

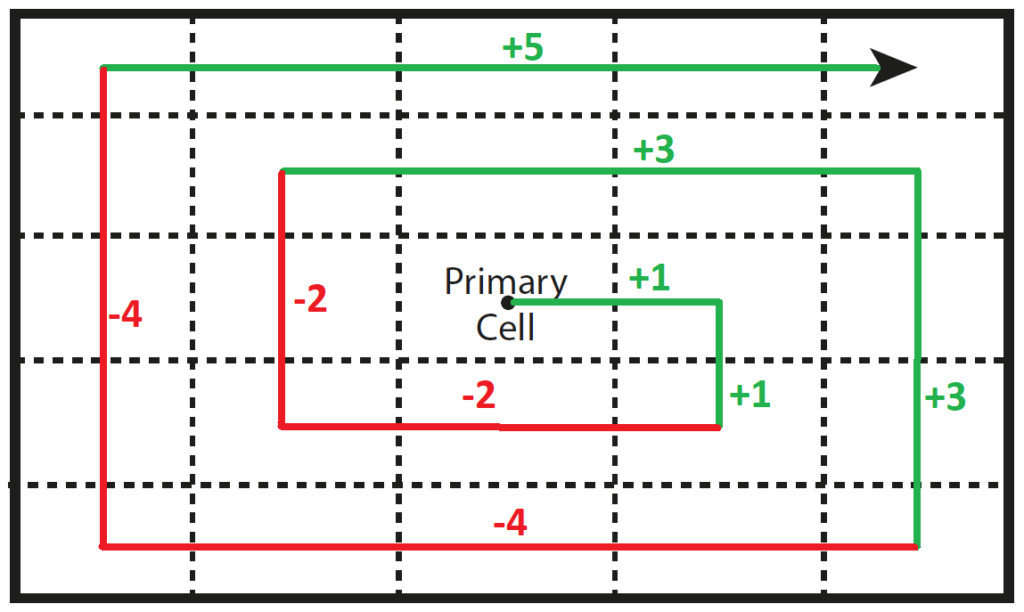
Which means we have to extend the sum S_n like this

$S_{n_{ext}} = \displaystyle S_n*\left(-1\right)^\left(S_n\right)+1 \quad \forall i \in \mathbb{N}$

What we have accomplished now is that we can create a list that tells how many times we have to step before the direction changes. We also know if it is a negative or positive step. The last missing part is the information about whether the step is in X or Y direction.

However, we won’t extend our formula further because we know that X-Y direction change ist alternating on every step.

We have done enough math now let’s jump to the implementation

Implementation

Now we are ready to implement the algorithm into code.

We will use c++ here for demonstration.

First of all you need to include two libraries to compile the full code example

#include <iostream>
#include <cmath>

<iostream> is a c++ library used for read/write operations from or to the standard stream. You can use the c library <stdio.h> instead if you want to make this a pure C program instead.

The <cmath> C library we need for calculating the power of a value and turning n to an absolute value. You can do these operations without the cmath library but the code would look pretty nasty.

Next, we create the matrix and some other related definitions, starting in the main() function.

int main()
{
    // this is used to calculate the matrix dimension
    const int ordersOfMagnitude = 4;

    // Calculated matrix dimension
    const int dim = (2 * ordersOfMagnitude) - 1;
    
    // x and y index of the center cell
    int center = std::ceil(dim / 2);

    // Definition of the matrix
    int matrix[dim][dim]{};

    // Setting the center cell to 1 and all other cells to 0
    for (int i = 0; i < dim; i++)
    {
        for (int j = 0; j < dim; j++)
        {
            if (i == center && j == center)
            {
                matrix[i][j] = 1;
            }
            else
            {
                matrix[i][j] = 0;
            }
        }
    }
}

The center variable is used to position the pointer to the center of the matrix as we want to start from there.

Now we want to visualize the matrix.

Create a separate function because this logic will be called many times.
It is important to put the drawMatrix function above the main() function otherwise the compiler will complain that the drawing function is missing.

/// <summary>
/// Visualizes the matrix inside the console using utf-8 characters
/// </summary>
/// <param name="matrix">The matrix variable</param>
/// <param name="dim">The dimension of the matrix</param>
void drawMatrix(int & matrix, const int dim)
{
    for (int x = 0; x < dim; x++) {
        for (int y = 0; y < dim; y++)
        {
            // accessing values in the matrix by indexing over pointer to reference
            if (*(&matrix + (y * dim) + x) == 1)
            {
                // this is a filled rectangle character which indicates the current position of the pointer
                std::cout << "[ " << char(-2) << " ]" << '\t';
            }
            else if (*(&matrix + (y * dim) + x) == -1)
            {
                // this draws a small sun character which indicates already visited cells in the matrix
                std::cout << "[ " << char(15) << " ]" << '\t';
            }
            else
            {
                // this is an empty matrix cell which has not been visited yet
                std::cout << "[ " << " " << " ]" << '\t';
            }
        }
        std::cout << std::endl << std::endl;
    }
}

int main()
{
   ...

We can call drawMatrix now inside the main function like this

// ... the logic before   

// visual output of the matrix
drawMatrix(matrix[0][0], dim);

Next comes the actual part where the pointer steps through the matrix in a spiral shape

    // ... the logic before   

    // Contains the result of the sum function
    int S_n = 0;
    // The while loop index which will be increased by one until the variable 'loops' has been reached
    int idx = 0;
    // Will be increased by one after each recalculation of the sum
    int stepIdx = 0;
    // Defines wether the pointer step goes in x or y direction
    char direction = 'x';
    // The number of steps in x direction beginning from the center
    int x = 0;
    // The number of steps in y direction beginning from the center
    int y = 0;
    // If this value has been reacht the while loop will be aborted
    int loops = (dim * dim) - 1;

    int* xy = &x;

    while(idx < loops)
    {
        // The left hand side of the sum formula
        S_n = std::abs(S_n) + 0.5 * (pow(-1, stepIdx) + 1);

        // multiplying the right hand side of the formula
        S_n *= pow(-1, S_n + 1);

        int n = std::abs(S_n);
        int next = S_n < 0 ? -1 : +1;

        stepIdx++;

        // assignes the x or y reference depending on step direction
        if (direction == 'x')
        {
            xy = &x;
            direction = 'y';
        }
        else
        {
            xy = &y;
            direction = 'x';
        }

        // steps to one direction until the direction changes
        for (int k = 0; k < n; k++)
        {
            int waitForInput = getchar();

            // Set value to "visited"
            matrix[center + x][center + y] = -1;
            // increase/decrease x or y by 1 depending on step direction 
            *xy += next;
            // Set value to "current position")
            matrix[center + x][center + y] = 1;
            // clear the terminal
            system("cls");
            // redraw the matrix
            drawMatrix(matrix[0][0], dim);

            // abort the loop if complete sequence has been reached
            if (++idx >= loops)
            {
                break;
            }

            std::cout << "Press Enter to continue ...";
        }
    }

    system("cls");
    drawMatrix(matrix[0][0], dim);
    std::cout << "Done!" << std::endl;

    return 0;
}

After that, you can compile and run your code.

Here is the full code


/// <summary>
/// Visualizes the matrix inside the console using utf-8 characters
/// </summary>
/// <param name="matrix">The matrix variable</param>
/// <param name="dim">The dimension of the matrix</param>
void drawMatrix(int & matrix, const int dim)
{
    for (int x = 0; x < dim; x++) {
        for (int y = 0; y < dim; y++)
        {
            // accessing values in the matrix by indexing over pointer to reference
            if (*(&matrix + (y * dim) + x) == 1)
            {
                // this is a filled rectangle character which indicates the current position of the pointer
                std::cout << "[ " << char(-2) << " ]" << '\t';
            }
            else if (*(&matrix + (y * dim) + x) == -1)
            {
                // this draws a small sun character which indicates already visited cells in the matrix
                std::cout << "[ " << char(15) << " ]" << '\t';
            }
            else
            {
                // this is an empty matrix cell which has not been visited yet
                std::cout << "[ " << " " << " ]" << '\t';
            }
        }
        std::cout << std::endl << std::endl;
    }
}

int main()
{
    // this is used to calculate the matrix dimension
    const int ordersOfMagnitude = 4;

    // Calculated matrix dimension
    const int dim = (2 * ordersOfMagnitude) - 1;
    
    // x and y index of the center cell
    int center = std::ceil(dim / 2);

    // Definition of the matrix
    int matrix[dim][dim]{};

    // Setting the center cell to 1 and all other cells to 0
    for (int i = 0; i < dim; i++)
    {
        for (int j = 0; j < dim; j++)
        {
            if (i == center && j == center)
            {
                matrix[i][j] = 1;
            }
            else
            {
                matrix[i][j] = 0;
            }
        }
    }

    // Visual output of the matrix
    drawMatrix(matrix[0][0], dim);

    // Contains the result of the sum function
    int S_n = 0;
    // The while loop index which will be increased by one until the variable 'loops' has been reached
    int idx = 0;
    // Will be increased by one after each recalculation of the sum
    int stepIdx = 0;
    // Defines wether the pointer step goes in x or y direction
    char direction = 'x';
    // The number of steps in x direction beginning from the center
    int x = 0;
    // The number of steps in y direction beginning from the center
    int y = 0;
    // If this value has been reacht the while loop will be aborted
    int loops = (dim * dim) - 1;

    int* xy = &x;

    while(idx < loops)
    {
        // The left hand side of the sum formula
        S_n = std::abs(S_n) + 0.5 * (pow(-1, stepIdx) + 1);

        // multiplying the right hand side of the formula
        S_n *= pow(-1, S_n + 1);

        int n = std::abs(S_n);
        int next = S_n < 0 ? -1 : +1;

        stepIdx++;

        // assignes the x or y reference depending on step direction
        if (direction == 'x')
        {
            xy = &x;
            direction = 'y';
        }
        else
        {
            xy = &y;
            direction = 'x';
        }

        // steps to one direction until the direction changes
        for (int k = 0; k < n; k++)
        {
            int waitForInput = getchar();

            // Set value to "visited"
            matrix[center + x][center + y] = -1;
            // increase/decrease x or y by 1 depending on step direction 
            *xy += next;
            // Set value to "current position")
            matrix[center + x][center + y] = 1;
            // clear the terminal
            system("cls");
            // redraw the matrix
            drawMatrix(matrix[0][0], dim);

            // abort the loop if complete sequence has been reached
            if (++idx >= loops)
            {
                break;
            }

            std::cout << "Press Enter to continue ...";
        }
    }

    system("cls");
    drawMatrix(matrix[0][0], dim);
    std::cout << "Done!" << std::endl;

    return 0;
}

This code is for demonstration purposes only and uses classic c/c++.

So when you’re going to put this into productive code, consider following the c++ core guidelines and use modern c++

Mathematical Model

Implementation

You Might Also Like

Jenkins CI: Running python scripts on a remote Windows nodes (machines)

Calcupiler – The Compile Time Calculator

Interval Tree